Risk Management: Forecasting your portfolio returns (Part 1)

How to measure your overall portfolio performance using equity curve.

Let’s keep it simple — this article is to guide you on how to estimate your portfolio returns. This is a part of a series that guides you on the basics of portfolio creation and risk management. No, we don’t tell you if any stocks are good or bad, and we don’t make any suggestions here — we teach you how to decide for yourself.

Important: Recap and sheet download link

This is what we’ve discussed so far:

Before we start, under the topic of Risk Management, we have looked at these things:

The calculations herein will be based on the calculations that we already had in our previous articles. You can download our MS Excel file if you want.

So… forecasting your investment returns?

Well, there’s not much to explain — but long story short, we will look into how you can forecast how your portfolio may perform in a year, given the historical returns of the assets in your portfolio. Since this is only the first part, we will only look into the simple forecast but do note that it is NOT SUFFICIENT for you to make a decision.

In order for you to make a well-informed decision, you will need (among others) to see the likeliness of multiple possibilities of returns. Put it this way, if you can just take the historical data and come up with an average return, and then actually get those numbers, there’ll be far too many billionaires in this world already. In reality, your investment can go as you expected, it can even go beyond that, or it could just slap you in the face.

To take into account these possibilities, you’ll need to see the range and likeliness of returns, which we will explain in later articles. For now, we’ll start with the basics.

How to forecast your portfolio returns?

Well, this can actually come off a bit simple. What you will need are:

1. The average daily return for each stock.

We’ve discussed this previously, but simply, all you need to do is see the percentage of change for each stock every day during your observation period. In our case, we chose these stocks over the course of a few years. Just a glimpse of it:

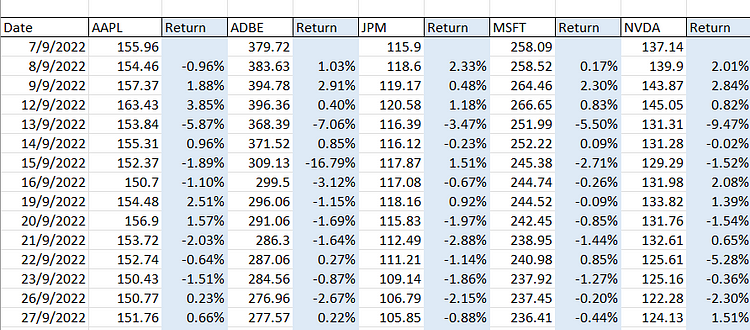
What we do next is look for the average daily returns for each stock. This is what it looks like:

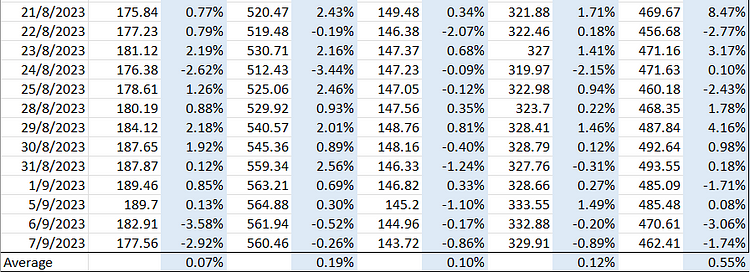
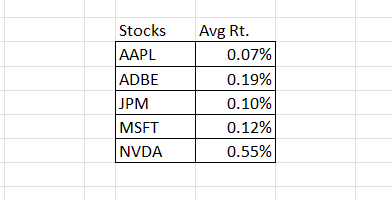
Now that we know the average daily returns for each stock over the course of one year (usually you’d need more than this, maybe 5 years, but we just use one year for the sake of making it simpler to teach), let’s arrange it in a proper table so it’d be easy to calculate things later on.

2. Weights of stocks in the portfolio

The weight of stocks in the portfolio depends on how much the stock values compared to the overall portfolio value. If Stock ABC is worth $10 out of a $100 portfolio, then its weight is 10% — because 10/100 is 0.10 or 10%. In our case, since we don’t use an actual portfolio, we made the weight up. Here are the made-up weights from our previous articles:

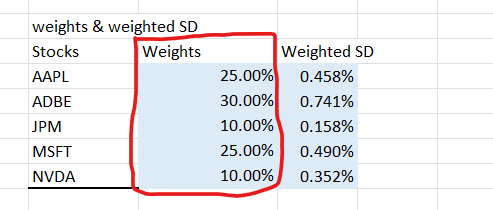
Now let’s put this into the table we just created alongside the average daily return.

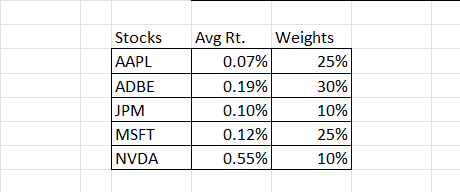
3. Expected annual return for each stock

Now, put the weights aside for a while and assume that you invested 100% of your money in only one of each stock from day one, over the course of one year — how would it look like? To do this, we will have to just multiply the average daily return of each stock by the number of days the market is open in a year. Here’s the formula:

Expected stock annual return = average daily return * number of days the market opens in a particular year

So, for 2023, our Google search made us believe that the market will be opened for 250 days in 2023, so it will be:

Expected stock annual return = average daily return * 250

This is how the updated table will look like:

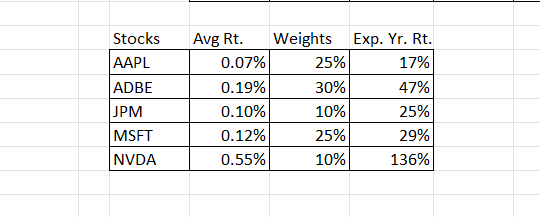
Now, Calculate the expected portfolio returns!

We’ve now gotten the ingredients required to see how our overall portfolio may look like over the year. What you need to do is get the total sum of Each stock’s expected annual return times the stock’s weight in the portfolio. Here’s what the formula would look like:

Expected annual portfolio return = (Stock A Exp. Yr. Rt. * Stock A weight) + (Stock B Exp. Yr. Rt. * Stock B Weight) + …

P/S: The three dots “…” in the formula are just “and so on”, which means that if you have more stocks in the portfolio, then add them up as well using the same step.

In our case, this is what it’d look like:

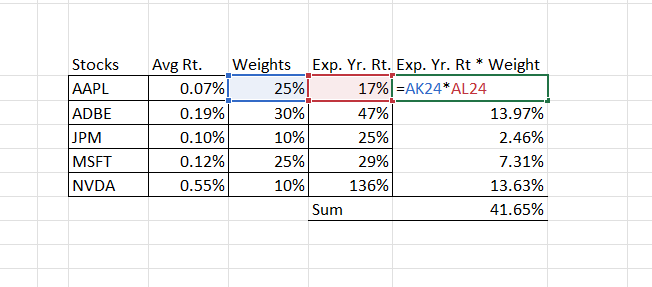
41.65% is the expected portfolio return over the course of one year of investing in this portfolio!

Easy, isn’t it? Of course, because that’s not all! We are just at the first step. However, don’t batter yourself up yet — even this is already a good milestone. Take some rest as we will get to the next steps in our later articles.

Bottom Line

Annual expected portfolio return is calculated by finding the total sum of Each stock’s expected annual return times the stock’s weight in the portfolio.
Expected annual portfolio return = (Stock A Exp. Yr. Rt. * Stock A weight) + (Stock B Exp. Yr. Rt. * Stock B Weight) + …
To find that, you’ll need to have the average daily return for each stock, the weights of stocks in the portfolio, and the expected annual return for each stock.
This is not all, as your portfolio can actually perform better or worse than the average expectation.
There are, however, expected returns with higher likeliness compared to others, which we will explore in later articles.

The key takeaways/market update is a series by AxeHedge, which serves as an initiative to bring compact and informative In/Visible Talks recaps/takeaways on leading brands and investment events happening around the globe.

Do keep an eye out for our posts by subscribing to our channel and social media.

None of the material above or on our website is to be construed as a solicitation, recommendation or offer to buy or sell any security, financial product or instrument. Investors should carefully consider if the security and/or product is suitable for them in view of their entire investment portfolio. All investing involves risks, including the possible loss of money invested, and past performance does not guarantee future performance.