The second triangle: the Descending Triangle
Read More
The Black-Litterman Model in Stock Trading- The Portfolio Optimizer

The Black-Litterman model has been an influential tool in the finance world since its introduction in 1990 by Fischer Black and Robert Litterman. With this model’s innovative approach to portfolio optimization, risk-return tradeoffs have become more intuitive and practical, fundamentally changing how asset allocation decisions are made.
Table of Contents
The Traditional Mean-Variance Framework

Before we delve into the workings of the Black-Litterman model, it is important to understand the limitations of its predecessor, the traditional Mean-Variance Optimization (MVO) approach. The MVO model, introduced by Harry Markowitz in the 1950s, seeks to construct an “efficient frontier” of portfolios that offer the highest expected return for a given level of risk, and vice versa.
However, MVO has a couple of significant issues. First, it relies heavily on historical returns to estimate future returns. This assumption can often lead to sub-optimal predictions. Second, MVO tends to suggest extreme long and short positions in a portfolio, due to its sensitivity to the input estimates. This is often risky for many novice investors.
The Black-Litterman Approach
The Black-Litterman model was developed to address these issues by reversing the MVO process. In contrast to starting with expected returns and deriving the optimal portfolio, Black-Litterman begins with a neutral portfolio – typically a market cap-weighted portfolio – and adjusts expected returns and covariances based on investors’ views.
Black-Litterman Optimizer
Numerous portfolio optimizers use the Black-Litterman model. Which enforces a sophisticated portfolio construction method that overcomes the problem of unintuitive, highly-concentrated portfolios, input sensitivity, and estimation error maximization, which are known shortcomings of mean-variance optimization. A Black-Litterman model calculates stable expected returns which are fed into a Mean-Variance Optimizer, which uses the returns in conjunction with different risk predictions and measures to calculate a robust portfolio.
Using a Bayesian approach, the Black-Litterman model combines the subjective views of a prediction model regarding the expected returns of one or more assets with the market equilibrium vector of expected returns to form a new, mixed estimate of expected returns.
Building using the Black-Litterman Model
Black-Litterman has three major components which are the equilibrium market portfolio, investor’s views, and confidence in views.
The Equilibrium Market Portfolio: The model starts with the assumption that the market portfolio is in equilibrium, i.e., the market portfolio’s asset allocation represents the collective views of all market participants.
Investor’s Views: These are subjective beliefs or expectations about certain assets or asset classes, which are incorporated to adjust the expected returns. The views could be absolute or relative, like “Stock A will return 7%” or “Stock B will outperform Stock C by 2%”.
Confidence in Views: The model also takes into account investor confidence in their views. Higher confidence in a particular view will have a more significant impact on the calculated expected returns.
The Mechanism
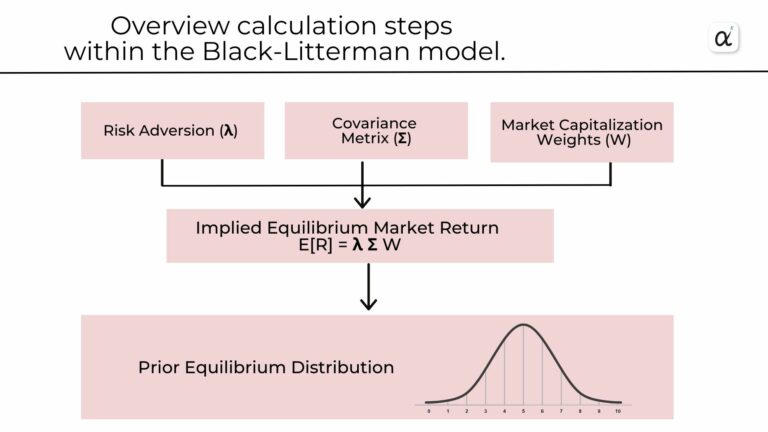
The equilibrium market portfolio is converted into equilibrium expected returns using the formula:

The investor’s views and confidence levels are combined in a matrix format, which is then used to adjust equilibrium expected returns. The new expected returns and covariances are used to derive the optimal portfolio, combining the equilibrium portfolio with the investor’s subjective views in a statistically robust way.
Implementing Black-Litterman as a Portfolio Optimizer
It involves several stages to implement the Black-Litterman model as a portfolio optimizer, including data collection, defining investor views, calculating expected returns, and finally optimizing the portfolio in order to achieve optimum performance.
Here is an overview of the process:
1. Data Collection.
The first step in any portfolio optimization is to gather data regarding the assets under consideration. This data should include the assets’ prices or returns over a significant period to ensure a robust analysis. Moreover, you should collect the market capitalization data for these assets in order to represent the market portfolio as well as any other information that will help you make your decision.
2. Calculate Market Portfolio Weights.
Use the market capitalization of each asset to calculate the market weights. The market weight of an asset is its market capitalization divided by the sum of the market capitalizations of all assets.
3. Estimated Covariance Matrix.
Use the returns data collected in Step 1 to estimate the covariance matrix of the assets. The covariance matrix provides a measure of the volatility and correlation between the assets.
4. Compute the Market Equilibrium Expected Returns.
Calculate the market equilibrium expected returns. This is done based on the assumption that the current market portfolio is in equilibrium.
The formula for calculating equilibrium returns is:
E[R] = λ Σ W
** λ is the risk aversion coefficient, Σ is the covariance matrix, and W is the market portfolio weights.
5. Define Investor's Views
Next, you need to articulate your views on the future performance of each asset in the portfolio. These views can be relative or absolute and are expressed in a way that can be represented mathematically. (e.g., asset A will outperform asset B) or absolute (e.g., asset A will return 5%). Encode these views mathematically in the form of a vector (Q) and a matrix (P). P is the matrix that represents the assets involved in each view, and Q is the vector that reflects the expected returns associated with each view.
6. Specify Confidence in Views.
Express the confidence you have in your views by assigning a measure of certainty or uncertainty to each view. This is usually expressed as a matrix (Ω), where the diagonal entry corresponds to the variance of the error in a view. The elements of Ω are typically determined by the uncertainty in each view which is often approximated as proportional to the variance of the residuals of the assets involved in the view. Larger values indicate higher confidence.
7. Combine Equilibrium Returns with Investor's Views
Next, you will combine the equilibrium returns with your views in order to calculate the combined expected returns. In order to do this, we use the following formula:

8. Portfolio Optimization
Last but not least, you can optimize the portfolio using the calculated expected returns and the covariance matrix, depending on the objective you are trying to achieve, whether it is maximizing returns with a given level of risk or minimizing risks with a given level of return.
In the Black-Litterman model, there are three aspects that make the Equilibrium Market Return Vector of great importance.
The first is stability. Unlike traditional portfolio optimization methods that rely heavily on historical return data, the Equilibrium Market Return Vector leverages the current market portfolio’s weights. This leads to more stable and reliable expected return estimates.
Second, less sensitivity to input estimation. With the model starting from the equilibrium portfolio and making small adjustments based on the investor’s views, the model is less likely to suggest extreme positions for the portfolio. It is often the case that the Black-Litterman model suggests more diversified portfolios than the traditional MVO model. In turn, this reduces the risk of portfolios.
Next is intuition. The equilibrium returns incorporate the collective wisdom of all market participants, encapsulating a vast amount of information about assets’ future prospects. Those returns are then recalculated based on a particular investor’s unique views in order to provide a more intuitive method for combining the market consensus with the expectations of an individual investor. It’s an intuitive and flexible way of reflecting personal beliefs in portfolio optimization.
Limitations and Considerations.
Despite the fact that Black-Litterman offers a more sophisticated approach to portfolio optimization, it does not come without its limitations. Models rely on the assumption of an initial equilibrium that may or may not exist in the real world, or which might not be easy to determine.
The implementation of the Black-Litterman model in a real-world environment scenario.
Implementing the Black-Litterman model in a real-world scenario requires several inputs, including data on market capitalizations, historical asset returns, and the investor’s views on expected returns.
Let's go through an example with a simplified three-asset portfolio: Stock A, Stock B, and Stock C.
1. Data Collection.
First, we gather historical returns data and market capitalization for each asset. Suppose the market capitalizations are:
Stock A: $500 B
Stock B: $300 B
Stock C: $200 B
Total market capitalization = $1 T
2. Calculate Market Portfolio Weights.
Next, we calculate the market capitalization weights:
Weight of Stock A = $500B / $1T = 0.50
Weight of Stock B = $300B / $1T = 0.30
Weight of Stock C = $200B / $1T = 0.20
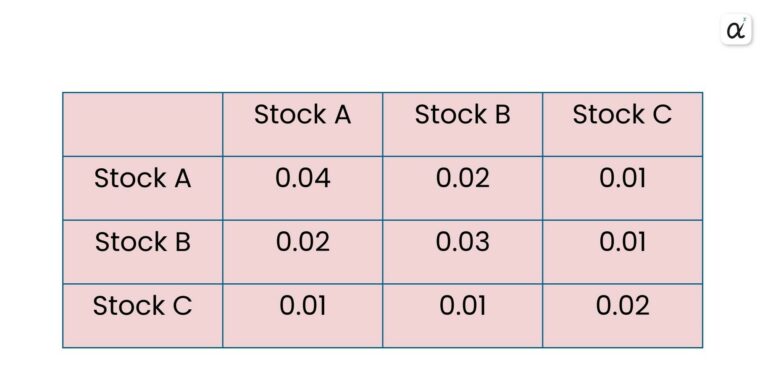
3. Estimated Covariance Matrix.
In order to simplify things, let’s assume we have the following covariance matrix from the historical returns data:
4. Compute the Market Equilibrium Expected Returns.
Let’s assume a risk aversion coefficient (λ) of 3. Next, we calculate equilibrium expected returns using the formula of E[R] = λ Σ W.
As a matter of convenience, let’s say the calculation results in the following:
The expected return of Stock A = 0.06
The expected return of Stock B = 0.04
The expected return of Stock C = 0.03
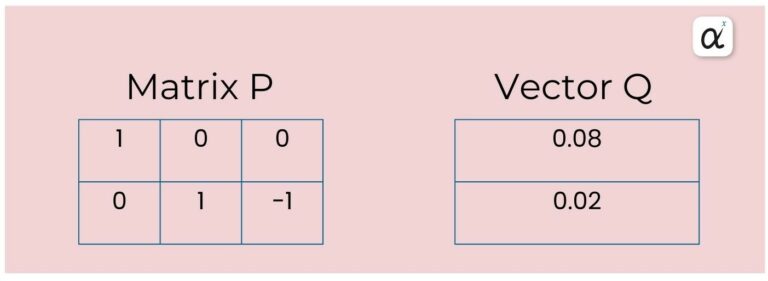
5. Define Investor's Views
Now, you articulate your views. Suppose you have the following views:
Stock A will return 0.08 (absolute view)
Stock B will outperform Stock C by 0.02 (relative view)
Matrix P and vector Q are used to express these views.
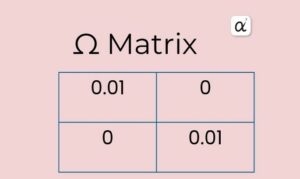
6. Specify Confidence in Views.
Next, you determine the level of confidence you have in each viewpoint. In this case, it can either be subjective or deduced from historical data.
Let’s say we have the following matrix:
7. Combine Equilibrium Returns with Investor's Views
Now, we compute the combined expected returns. Assuming a scalar τ of 0.05, we use the formula:
E[R’] = [τΣ^-1 + P’Ω^-1P]^-1 [τΣ^-1 E[R] + P’Ω^-1Q]
The calculation results are as the following:
The expected return of Stock A = 0.072
The expected return of Stock B = 0.045
The expected return of Stock C = 0.032
These values suggest that based on the market’s equilibrium condition and the investor’s personal views, the anticipated returns of Stocks A, B, and C are 7.2%, 4.5%, and 3.2% respectively. This calculation gives a more balanced expected return compared to the original equilibrium returns and the investor’s views
**The next step would be to use these expected returns and the covariance matrix of the assets’ returns to construct an optimal portfolio. This could be achieved through various portfolio optimization techniques, such as Mean-Variance Optimization, which aims to maximize return for a given level of risk or minimize risk for a given expected return.
In a Nutshell
The Black-Litterman model creates stable returns, based on the unique insights of a prediction model, which overcomes input sensitivity. Black-Litterman’s model also mitigates the problem of estimation error maximization by spreading the errors over the entire vector of expected returns, thus enhancing the stability of the predicted returns.
The Black-Litterman returns are essential when generating stable, mean-variance efficient portfolios. Conversely, classical expected return predictions based on historical asset returns, equal mean returns, or risk-adjusted equal mean returns lead to extreme portfolios.
Portfolios with extreme positions have large long and short positions when no constraints apply, and portfolios with a small number of assets when long-only asset positions are limited.
Nevertheless, this is the process of implementing the Black-Litterman model as a portfolio optimizer in accordance with the Black-Litterman model. As a matter of fact, there are several subtleties and nuances to the model that need to be taken into account, particularly when it comes to defining views and the risk aversion coefficient λ, as well as the scaling factor τ. Considering these factors is crucial when calibrating a model to ensure that it accurately reflects the investor’s outlook and level of risk tolerance, as well as their appetite.
The key takeaways/market update is a series by AxeHedge, which serves as an initiative to bring compact and informative In/Visible Talks recaps/takeaways on leading brands and investment events happening around the globe.
Do keep an eye out for our posts by subscribing to our channel and social media.
None of the material above or on our website is to be construed as a solicitation, recommendation or offer to buy or sell any security, financial product or instrument. Investors should carefully consider if the security and/or product is suitable for them in view of their entire investment portfolio. All investing involves risks, including the possible loss of money invested, and past performance does not guarantee future performance.
Trading Dow Pattern the Triangle Pattern (Part 1)
The first triangle: the Ascending Triangle
Read MoreFunds: Equity Funds (Part 3)
How to choose between equity funds based on companies’ earnings...
Read More



